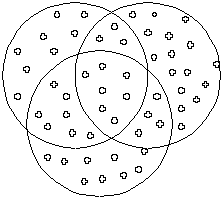
Nous classons les objets mentaux par ensemble. Un ensemble est composé d'éléments qui ont une propriété en commun. La crainte, l'amitié, le patriotisme appartiennent à l'ensemble "sentiment".

les ensembles "cube", "bois", "bleu"

Un objet mental peut appartenir à plusieurs ensembles à la fois, ainsi les cubes en bois bleus appartiennent aux ensembles cube, bois et bleu. Ils appartiennent à l'ensemble "cube & bois & bleu".

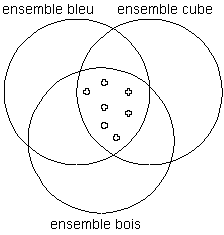
l'ensemble "cube & bois & bleu"

Nous classons les objets mentaux en ensembles parce qu'il est plus simple de manipuler des ensembles que la totalité des objets mentaux. Mais l'ensemble est un concept, c'est un objet mental différent des éléments qui le constitue, c'est un objet mental hiérarchiquement de niveau supérieur aux éléments. Les propriétés des éléments ne s'appliquent pas à l'ensemble, qui a d'autres propriétés. Une foule, un ensemble d'individus, a un comportement différent de celui des individus. L'ensemble (ce qui comprend tous les éléments), n'est pas un élément de l'ensemble. Confondre les deux conduit au paradoxe tel que: je dis "tous les belges sont des menteurs".

Lorsque nous manipulons des ensembles nous devons réaliser que ce sont des concepts, c'est à dire des objets mentaux à composante réelle faible ou nulle, et que ces ensembles représentent des classes d'objets mentaux, mais non les objets mentaux eux-mêmes qui sont les éléments.

Nous devons réaliser que ce que nous désirons changer, modifier, c'est un élément et non un ensemble.

Tout objet mental est conçu par comparaison, par contraste. Dans un ensemble nous classons des objets mentaux tels que, amour, haine, indifférence. Nous ne classons pas seulement des objets mentaux qui ont la même propriété mais aussi des propriétés contraires. Ce classement correspond à un type d'ensemble particulier appelé groupe en mathématique. La théorie des groupes peut nous aider à comprendre comment nous classons les objets mentaux dans un ensemble, en n'oubliant pas que cette théorie ne s'applique parfaitement qu'à des objets mentaux mathématiques.

Un groupe est un ensemble d'éléments dont les éléments ont des propriétés particulières décrites par des lois, les lois de composition, d'invariance du résultat, de l'élément neutre et de la symétrie.

Par définition, un groupe se compose d'éléments qui ont en commun une loi de composition, telle que la composition de plusieurs éléments donne un élément du groupe. Les quelques exemples suivants illustrent cette loi.

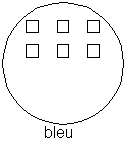
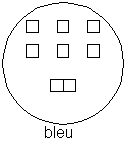
loi de composition (bleu) du groupe "bleu"

Le groupe "bleu" a pour loi de composition "bleu", c'est à dire que tout élément composé de plusieurs éléments est "bleu".

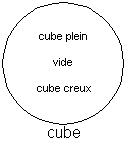
Par contre l'ensemble "cube" n'est pas un groupe. Tout élément composé de plusieurs éléments n'est plus un cube.

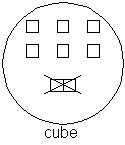
loi de composition (cube)

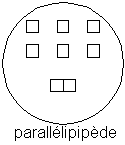
Je peux définir un groupe "parallélépipède aligné" dont la loi de composition est l'assemblage des objets suivant un axe horizontal, en composant les éléments d'après cette loi, j'obtiens toujours des parallélépipèdes.

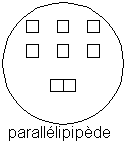
loi de composition (parallélépipède aligné) du groupe

De même un ensemble de nombres dont la loi de composition est l'addition, forment un groupe, en additionnant plusieurs éléments on obtient un nombre.

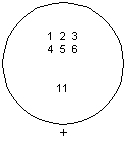
loi de composition (addition) du groupe "nombre"

De même l'ensemble des déplacements possibles entre villes dont la loi de composition est le déplacement successif d'une ville à l'autre, forment un groupe, en se déplaçant successivement on obtient un déplacement.

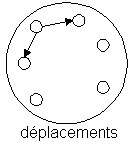
Une autre propriété des éléments d'un groupe est l'invariance du résultat de composition. Si on compose les éléments d'un groupe suivant la loi de composition selon des séquences différentes, on obtient toujours le même type d'élément. Peu importe l'ordre dans lequel on additionne les nombres, 5+6 = 6+5, on assemble n'importe quels parallélépipèdes deux à deux, on se déplace d'une ville à l'autre directement ou en passant par d'autres villes,  le nouvel élément obtenu reste du même type.

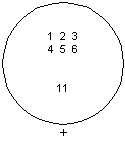
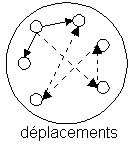
invariance du résultat de composition

Un groupe contient un élément neutre, tel que sa composition avec un autre élément donne cet élément. 5 + 0 =5, l'immobilité n'ajoute rien à un déplacement.

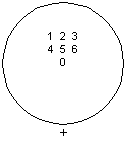
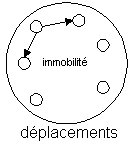
élément neutre d'un groupe

Pour chaque élément du groupe existe un autre élément symétrique tel que sa composition avec un autre élément donne l'élément neutre. 5 - 5 = 0, se déplacer et revenir au même endroit donne le même résultat que l'immobilité.

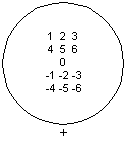
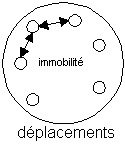
éléments symétriques d'un groupe