
Si j'ai décidé d'aller à Paris et que je constate que je me dirige vers Lille, j'ai fait une faute. C'est une maladresse due à un manque de connaissance ou de moyens, ou due à l'utilisation de moyens inadéquats.
Si je mesure plusieurs fois la distance parcourue par ma voiture avec un mètre d'une longueur de 1 mètre, j'obtiens plusieurs grandeurs différentes: 100,1 mètres, 99,8 mètres, etc. En effectuant suffisamment de mesures je peux calculer une grandeur moyenne, 100 mètres, et une erreur probable qui m'indique que la distance réelle est supérieure à 99,6 mètres et inférieure à 100,4 mètres. Les différences entre les mesures sont dues au hasard, et non à une faute. Je ne peux jamais connaître la distance réelle, mais je peux dire que la distance est de 100 mètres + ou - 0,4 mètre. L'erreur probable est de 0,4 mètre.
Mais la confiance que je peux avoir dans les différentes grandeurs mesurées dépend de la précision de mon mètre. Si je compare un mètre de couturière et un mètre métallique, je constate que les deux longueurs ne sont pas les mêmes. Il n'existe au monde qu'un seul mètre exact, c'est une règle de platine conservée à Paris dans une chambre à température constante. Tous les autres mètres sont des copies dont la différence de grandeur est garantie inférieure à une certaine grandeur. Supposons que mon mètre soit garanti à 1 cm. je suis donc certain que mon mètre mesure réellement au moins 0,99 m. et au plus 1,01 m., soit 1 m. +ou- 0,01 m., soit 1 m. +ou- 1%. Ce 1% est l'erreur absolue de mon mètre et je connais cette erreur.
Dans la mesure de la distance parcourue par la voiture nous devons tenir compte de cette erreur absolue du mètre. Nous pouvons dire que la distance mesurée est de 100 x (1 m. +ou- 0,01 m.) = 100 m. +ou- 1 m. = 100 m. +ou- 1%. Ce 1% est l'erreur relative de la mesure. Si avec le même mètre je mesure la largeur d'une chaise 1 x (0,4 m +ou- 0,01 m.) = 0,4 m. +ou- 0,01 m. = 0,4 m. +ou- 2,5%. Ce 2,5% est l'erreur relative de la mesure de la largeur de la chaise. je ne connais pas l'erreur réelle, mais je suis certain qu'elle est inférieure à 2,5%. En tenant compte de l'erreur probable et de l'erreur relative, je peux dire que la distance parcourue par la voiture est comprise entre 98,6 et 101,4 mètres.
Cela n'a pas de signification de dire que la distance est de 100 mètres. Cela n'a pas de signification de dire que la distance est de 100 +ou- 0,4 mètres si l'erreur relative est de 1 mètre. Un résultat, même calculé en moyenne, n'a de valeur que si on donne le degré de confiance.
Il n'est pas possible de connaître la réalité, il y a toujours une erreur dans l'appréhension de la réalité. On peut réduire cette erreur dans les limites de nos possibilités, on peut négliger cette erreur en portant un jugement de valeur. On a cru longtemps qu'avec le progrès on pourrait reculer indéfiniment les limites de nos possibilités et arriver à une erreur nulle, mais la physique de l'infiniment petit nous a fait découvrir qu'il existe une limite à toute mesure, limite qui est négligeable dans notre monde mais importante dans le monde de l'infiniment petit.
Une action est prise pour obtenir un résultat. Nous savons quand commence l'action et nous prévoyons quand elle sera terminée. Mais comment évolue le résultat dans le temps? Est-il obtenu directement?

Le résultat progresse au fur et à mesure que l'action progresse dans le temps. La progression du résultat est le cumul des résultats instantannés dus aux actions instantannées, ou en terme mathématique le résultat est l'intégrale de l'action. Le résultat obtenu par l'action modifie l'état ou la situation d'une chose. L'évolution de la situation ou de l'état est le taux de changement de la situation, ou en terme mathématique l'évolution de la situation est la dérivée de la situation.

Il peut s'écouler un certain temps avant que le résultat n'apparaisse et pendant lequel il ne se passe rien. Ce temps entre le début de l'action et le début du résultat est le retard.

le retard
Il se peut aussi qu'une série d'action soit nécessaire pour obtenir le résultat. Ces actions successives obéissent à une règle qui détermine la prochaine action en fonction du résultat obtenu précédemment. On constate que le résultat démarre directement, mais que le résultat final n'est obtenu qu'après un certain temps que nous appellerons délai. C'est ce phénomène de délai, dont on ne tient souvent pas compte dans les prévisions, qui fait que souvent le résultat final est obtenu après la date prévue.
le délai
Pour mieux comprendre prenons l'exemple d'une gestion de stock. Je dois obtenir le résultat d'un stock de 1.000 pièces par une action de commande de 250 pièces par mois.
évolution des commandes et du stock en fonction du temps
Le diagramme indique l'évolution du résultat en fonction du nombre de semaines. La quantité désirée en stock est atteinte après quatre semaines, mais je constate que le stock augmente indéfiniment; en effet je n'ai pas de règle qui me signale que je dois arrêter mon action lorsque le stock atteint la grandeur de 1.000 pièces. Je continue indéfiniment à commander 250 pièces par semaine.
nombre de pièces commandées en fonction du stock
Je dois donc utiliser une règle, qui au départ permette mon action de commande de 250 pièces par semaine et, qui réduise mon action à zéro lorsque le stock atteint le résultat désiré de 1.000 pièces.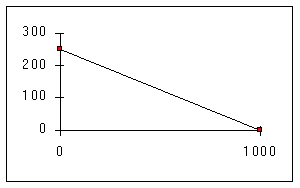
nombre de pièces commandées en fonction du stock
En utilisant cette règle le stock se limite automatiquement à 1.000 pièces, mais je constate que ce résultat n'est atteint qu'après un délai de 10 semaines.
évolution des commandes et du stock en fonction du temps
Si j'avais utilisé une autre règle je pourrais obtenir une évolution du stock comme indiqué dans le diagramme suivant où le résultat devient instable et oscille autour de la grandeur 1.000.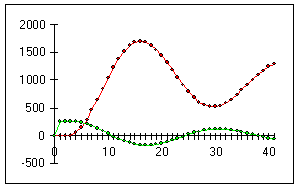
évolution des commandes et du stock en fonction du temps
La
stabilité du résultat est une propriété qui indique que le résultat est permanent, qu'il ne varie pas en fonction du temps après une certaine période. La courte période pendant laquelle il y a passage de la situation initiale à la situation finale est appelée période transitoire.La qualité du résultat est une mesure des propriétés du résultat par rapport à des propriétés définies comme références. Cette mesure se fait par un jugement de vérité accompagné d'un jugement de valeur sur l'erreur. La qualité est du domaine du passé, elle attribue une grandeur à un objet ou une action passée. Il est possible d'attribuer une qualité à un objet ou une action future; c'est la fiabilité. C'est la confiance que l'on peut avoir qu'un objet remplira sa fonction pendant un certain temps ou qu'une action donnera un résultat prévu.
La fiabilité fait intervenir le jugement rationnel à partir de table de résultats d'essais: ainsi l'action de détecter une lampe de 20 mm. qui brûle parmi deux autres a une fiabilité de 99,83 %. Une suite d'actions réalisées en série a une fiabilité moindre que chaque action prise séparément, elle est égale au produit des fiabilités respectives. Ainsi l'action de détecter deux fois l'allumage d'une lampe a une fiabilité de 99,66%. Par contre des actions menées en parallèle ont une fiabilité plus grande que les fiabilités respectives, elle est égale à 1-(1-p)². L'action de détecter l'allumage d'une lampe par deux hommes a une fiabilité de 99,9997%.
Cette notion de fiabilité implique qu'aucun individu n'est capable de mener une action qui donne un résultat exact, il y a toujours une erreur. Toutefois cette erreur peut être diminuée par le travail en équipe. Ainsi si un premier individu exécute une tâche avec une fiabilité de 95%, le taux d'erreur est de 5%. Mais si un second individu vérifie ce travail avec une fiabilité de 95%, si le premier corrige ses erreurs avec une fiabilité de 95% et si le second vérifie le travail corrigé avec une fiabilité de 95%, la fiabilité du résultat final est de 99,7%, c'est à dire un taux d'erreur de 0,3% au lieu des 5% initiaux. Pour des individus travaillant avec une fiabilité supérieure le taux d'erreur est indiqué dans le diagramme suivant. On atteint une fiabilité de 99,999% pour certains objets par un contrôle de qualité à toutes les étapes de fabrication.

erreur sur un travail vérifié en fonction de la fiabilité
La même notion de fiabilité s'applique aux relations humaines, mais cette notion est différente de celle du langage courant. Dans le langage courant "fiable" veut dire sûr, homme de confiance, sur lequel on peut compter et cette définition sous-entend qu'il n'y a jamais d'erreur. Nous définirons fiable comme sûr à 95%.Nous utiliserons le terme workmanship pour définir la confiance en la capacité d'un individu de réaliser un travail exact sans vérification. La confiance est de 100% mais est remise en question par des examens ou supprimée suite à une faute. Le workmanship fait intervenir un jugement de valeur. Ainsi un pilote d'avion militaire fait entièrement confiance à son mécanicien de sol pour la préparation de son avion. Un jour le pilote est redescendu de son avion après un vol avec en main la goupille de sécurité du siège éjectable que son mécanicien avait oublié d'enlever. Le mécanicien a remis immédiatement son préavis, car il savait que plus aucun pilote n'aurait confiance en lui, et pourtant il y avait peu de chance qu'il refasse la même faute.
Copyright 2001 by Stéphane Coël - L'intelligence émotionnelle et rationnelle dans l'action